On Spectrum of the Weakly Zero-Divisor Graph

Authors

  • Asif Imtiyaz Ahmad Khan Department of Mathematics, Aligarh Muslim University, Aligarh, 202002, India
  • Muzibur Rahman Mozumder Department of Mathematics, Aligarh Muslim University, Aligarh, 202002, India
  • Mohd Rashid Department of Mathematics, Aligarh Muslim University, Aligarh, 202002, India
  • Abu Zaid Ansari Department of Mathematics, Faculty of Science, Islamic University of Madinah, Madinah, K.S.A. https://orcid.org/0000-0001-6139-7521 (unauthenticated)
  • Faiza Shujat Department of Mathematics, College of Science, Taibah University, Madinah, K.S.A.

DOI:

https://doi.org/10.37256/cm.6520258269

Keywords:

ring of integers modulo <i>n</i>, weakly zero-divisor graph, spectrum of graph, Seidel Laplacian and Seidel signless Laplacian spectrum

Abstract

Let us consider the finite commutative ring R, whose unity is 1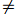mceclip0-90ffec1c7fda5a9d3c8d0e1405cd1d3d.png0. The weakly zero-divisor graph, denoted by WΓ(R), is an undirected graph whose distinct vertices c1 and c2 are adjacent if and only if, there exist r ∈ ann(c1) and s ∈ ann(c2) that satisfy the condition rs = 0. This article finds the Seidel Laplacian and Seidel signless Laplacian spectrum for the graph WΓ(Zn) for various values of n.

References

Downloads

Published

2025-09-24

Issue

Contemporary Mathematics, Volume 6 Issue 5 (2025), 5368-7533

Section

Research Article

License

Copyright (c) 2025 Abu Zaid Ansari, et al.

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

1.
On Spectrum of the Weakly Zero-Divisor Graph. Contemp. Math. [Internet]. 2025 Sep. 24 [cited 2025 Dec. 24];6(5):6812-31. Available from: https://ojs353.mebyme.cn/index.php/CM/article/view/8269