Structure of Algebras Satisfying an ω-Polynomial Identity of Degree Six

Authors

  • Hamed Ouedraogo Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso https://orcid.org/0009-0002-1505-3933
  • Daouda Kabré Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso https://orcid.org/0009-0004-9862-2226
  • Abdoulaye Dembega Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso
  • André Conseibo Department of Mathematics, Norbert Zongo University, Koudougou, Burkina Faso https://orcid.org/0000-0001-7424-273X

DOI:

https://doi.org/10.37256/cm.6220256453

Keywords:

idempotent, Peirce decomposition, <i>ω</i>-polynomial identity, Bernstein algebras, train algebras, evolution algebra

Abstract

This paper is devoted to the study of a class of commutative non-associative algebras characterized by the identity: 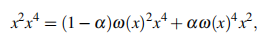mceclip0-6675dc5b2f5ea0fb8828593d9e755666.png

where α ∈ [0, 1]. In this study, we strongly use the Peirce decomposition technique. This allowed us to determine the conditions for an algebra of this class to be Bernstein, principal train, or evolution.

References

Downloads

Published

2025-03-19

Issue

Contemporary Mathematics, Volume 6 Issue 2 (2025), 1380-2725

Section

Research Article

License

Copyright (c) 2025 Hamed Ouedraogo, Daouda Kabr´e, Abdoulaye Dembega, Andr´e Conseibo

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

1.
Structure of Algebras Satisfying an ω-Polynomial Identity of Degree Six. Contemp. Math. [Internet]. 2025 Mar. 19 [cited 2025 Dec. 24];6(2):1914-25. Available from: https://ojs353.mebyme.cn/index.php/CM/article/view/6453