Solvability of a Doubly Singular Boundary Value Problem Arising in Front Propagation for Reaction-Diffusion Equations

Authors

  • Cristina Marcelli Department of Industrial Engineering and Mathematical Sciences, Polytechnic University of Marche, Via Brecce Bianche 12, Ancona 1-60131, Italy https://orcid.org/0000-0002-6614-9276

DOI:

https://doi.org/10.37256/cm.6120256084

Keywords:

singular boudary value problems, reaction-diffusion-convection equations, travelling wave solutions, degenerate parabolic equations, speed of propagation

Abstract

The paper deals with the solvability of the following doubly singular boundary value problem

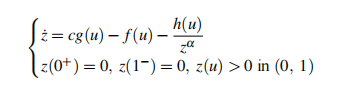
mceclip0-c9f177fad2ec0f7fef19793e3546d07c.png

naturally arising in the study of the existence and properties of travelling waves for reaction-diffusion-convection equations

governed by the p-Laplacian operator. Here c, α are real parameters, with α > 0, and f, g, h are continuous functions in [0, 1], with

h(0) = h(1), h(u) > 0 in (0, 1).

References

Downloads

Published

2024-12-31

Issue

Contemporary Mathematics, Volume 6 Issue 1 (2025), 1-1379

Section

Research Article

License

Copyright (c) 2024 Cristina Marcelli.

Creative Commons License

This work is licensed under a Creative Commons Attribution 4.0 International License.

How to Cite

1.
Solvability of a Doubly Singular Boundary Value Problem Arising in Front Propagation for Reaction-Diffusion Equations. Contemp. Math. [Internet]. 2024 Dec. 31 [cited 2025 Dec. 24];6(1):135-4. Available from: https://ojs353.mebyme.cn/index.php/CM/article/view/6084