Maximal Convergence by Faber Series in Morrey-Smirnov Classes with Variable Exponents
DOI:
https://doi.org/10.37256/cm.6120255234Keywords:
rate of convergence, morrey-smirnov classes with variable exponents, faber series, dini-smooth curvesAbstract
In this paper, we assume that G is a domain bounded by Γ Dini-smooth curve and R > 1 is the largest number such that a function f is analytic inside the level curve ΓR in the exterior of Γ. By taking the function f in the Morrey-Smirnov classes with variable exponents 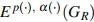 , we obtain a rate of maximal convergence of the nth partial sums of the Faber series of the function f in the uniform norm on the closure of G. Here the rate of maximal convergence depends on the best approximation number
, we obtain a rate of maximal convergence of the nth partial sums of the Faber series of the function f in the uniform norm on the closure of G. Here the rate of maximal convergence depends on the best approximation number 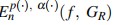 .
.
References
Downloads
Published
2025-02-25
Issue
Section
Research Article
License
Copyright (c) 2025 Burcin Oktay.

This work is licensed under a Creative Commons Attribution 4.0 International License.
How to Cite
1.
Maximal Convergence by Faber Series in Morrey-Smirnov Classes with Variable Exponents. Contemp. Math. [Internet]. 2025 Feb. 25 [cited 2025 Dec. 24];6(1):1361-79. Available from: https://ojs353.mebyme.cn/index.php/CM/article/view/5234
